Matemáticas 2. Trigonometria. COBAO 04 EL TULE. SEMESTRE. 2020-A. Josh Brandon Ruiz Cruz. GRUPO: 205

MATEMÁTICAS II. TRIGONOMETRIA. 

COBAO 04 EL TULE

Nombre del alumno: Ruiz Cruz Josh Brandon

Nombre del docente: Alejandro Enrique Vasquez Martinez

GRUPO: 205

Semestre: 2020-A

26/03/20 oaxaca de juarez oaxaca

RESUMEN: Clasificación y formas de medición de ángulos. conversión de ángulos

Sistemas de Medición de Ángulos

En la medida de ángulos, y por tanto en trigonometría, se emplean cuatro unidades, si bien la más utilizada en la vida cotidiana es el Grado sexagesimal, en matemáticas es el Radián la más utilizada, y se define como la unidad natural para medir ángulos, el Grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción. Radián: unidad angular natural en trigonometría, será la que aquí utilicemos. En una circunferencia completa hay 2π radianes. Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados. Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales. Horario: su unidad de medida es el ángulo de 1 hora, que equivale a la sexta parte del ángulo recto.  Relación entre los Sistemas de medición de ángulos: 180º -------- π rad. ----------- 200G----------- 12 hs

RESUMEN: Las razones trigonométricas

Razones trigonométricas en un triángulo rectángulo

Seno

El seno del ángulo B es la razón entre el cateto opuesto al ángulo y la hipotenusa. Se denota por sen B.

Coseno

El coseno del ángulo B es la razón entre el cateto adyacente o contiguo al ángulo y la hipotenusa. Se denota por cos B.

Tangente

La tangente del ángulo B es la razón entre el cateto opuesto al ángulo y el cateto adyacente al ángulo. Se denota por tan B o tg B.

Cosecante

La cosecante del ángulo B es la razón inversa del seno de B.

Se denota por csc B o cosec B.

Secante

La secante del ángulo B es la razón inversa del coseno de B.

Se denota por sec B.

Cotangente

La cotangente del ángulo B es la razón inversa de la tangente de B.

Se denota por cot B o ctg B.

RESUMEN: ángulos de elevación y depresión

Ángulos de depresión y de elevación 

El término ángulo de progresión denota al ángulo desde la horizontal hacia arriba a un objeto. Una línea de vista para el observador estaría sobre la horizontal.

El término ángulo de depresión denota al ángulo desde la horizontal hacia abajo a un objeto. Una línea de vista para el observador estaría debajo de la horizontal.

Dese cuenta que el ángulo de progresión y el ángulo de depresión son congruentes .

RESUMEN DE LAS CARACTERÍSTICAS PARA LA MEDICIÓN DE ÁNGULOS EN TRIGONOMETRIA.

 (ángulos de referencia) Características

 Digamos Que θ Es Un ángulo de ningún cuadrante en s posición Estándar. Su ángulo de referencia es el ángulo agudo a formado por el lado terminal de θ y el eje horizontal. 

 Cuadrante I: El ángulo dado y el ángulo de referencia son el mismo ángulo. α = θ

FÓRMULA PARA EL ÁNGULO DE REFERENCIA ΘR

θR se mide en base de la posición de un ángulo dado en cualquiera de los cuatro cuadrantes de un plano rectangular: 

CUADRANTE I

θR = θ

CUADRANTE II

θR = 180⁰ – θ (grados) o θR = π – θ  (radianes)

CUADRANTE III

θR = θ – 180⁰ (grados) o θR = θ – π (radianes)

CUADRANTE IV

θR = 360⁰ – θ (grados) o θR = 2π – θ (radianes)

RESUMEN DEL CIRCULO UNITARIO Y FUNCIONES TRIGONOMÉTRICAS

La definición en el círculo unitario nos permite extender el dominio de seno y coseno a todos los números reales. El proceso para determinar el seno o coseno para cualquier ángulo $\theta$theta es como sigue:

1. Empezando en $(1,0)$left parenthesis, 1, comma, 0, right parenthesis, nos movemos a lo largo del círculo en sentido contrario a las manecillas del reloj hasta que el ángulo que se forma entre tu posición, el origen y el eje $x$x positivo sea igual a $\theta$theta.
2. $\sin(\theta)$sine, left parenthesis, theta, right parenthesis es igual a la coordenada $y$y de tu punto, y $\cos(\theta)$cosine, left parenthesis, theta, right parenthesis es igual a la coordenada $x$x.

$y$$x$$(\cos(\theta),\sin(\theta))$$\theta$$O$$\cos(\theta)$$\sin(\theta)$$\small 1$$\small 1$$\small{-1}$$\small{-1}$

Las demás funciones trigonométricas pueden evaluarse a partir des su relación con seno y coseno.

GRÁFICAS DE FUNCIONES TRIGONOMÉTRICAS

Algunas de las propiedades de una gráfica de las funciones trigonométricas son: dominio, máximo, asíntotas, periodo, alcance, etc.

Las funciones trigonométricas son: y=sen(x), y=cos(x), y=tan(x), y=cot(x), y=csc(x) o y=sec(x), en donde lo que está en el paréntesis es el dominio y “y” es el alcance.

CARACTERÍSTICAS DE LA GRÁFICA DE  y = sen(x)

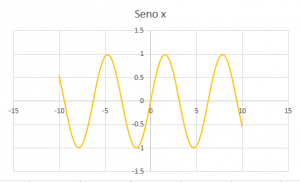
El ciclo de la función seno comienza en 0 y termina en 2π.

Dominio: el conjunto de números reales

Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.

Cruza el eje de “y” en (0,0)

El eje de referencia es: eje “x”.

El punto máximo es:  (π/2,1)

El punto mínimo es: (3π/2,-1)

Su período: 2π.

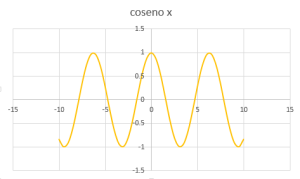
CARACTERÍSTICAS DE LA GRÁFICA DE  y = cos(x)

El ciclo fundamental de la función coseno del ángulo comienza en 0 y termina en 2π.

Dominio: el conjunto de números reales.

Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.

Cruza el eje de “y” en: (0,1)

El eje de referencia es: el eje “x”

El punto máximo es:  (0,1) y (2π,1)

El punto mínimo es: (π,-1)

Su período: 2π

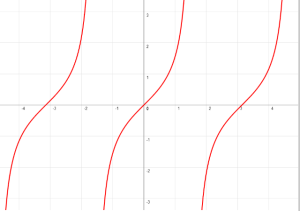
CARACTERÍSTICAS DE LA GRÁFICA DE  y = tan(x)

El ciclo fundamental de la función tangente del ángulo comienza en -π/2 y termina en π/2.

Tiene asíntotas en el ciclo.

Dominio: toda x diferente a (π/2)±nπ

Alcance: el conjunto de todos los números reales.

Cruza el eje de “y” en  (0,0)

El eje de referencia es: el eje “x”

El punto máximo es:

El punto mínimo es:

Su período: π

Asíntotas: x=±π/2

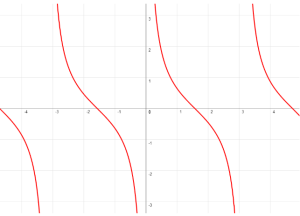
CARACTERÍSTICAS DE LA GRÁFICA DE  y = cot(x)

El ciclo fundamental de la función cotangente del ángulo comienza en 0 y termina en π.

Tiene asíntotas en el ciclo.

Dominio: toda x diferente a ±nπ

Alcance: el conjunto de todos los números reales.

No cruza el eje de “y”

El eje de referencia es: el eje “x”.

Su período: π

asíntotas: x=±nπ

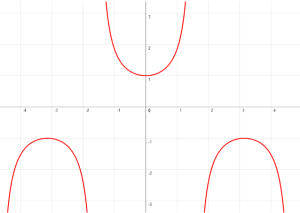
CARACTERÍSTICAS DE LA GRÁFICA DE  y = sec(x)

El ciclo fundamental de la función secante del ángulo comienza en -π/2 y termina en 3π/2.

Tiene tres asíntotas verticales.

Dominio: el conjunto de números reales excepto los múltiplos impares de π/2

Alcance: el conjunto de todos los números reales menores menores o iguales que –1 y todos los números mayores o iguales que 1

Cruza el eje de “y” en (0,1)

El eje de referencia es: el eje “x”

El punto máximo es:  (π,-1)

El punto mínimo es:  (0, 1)

Su período: 2π

Asíntotas: x=-π/2, x=π/2 y x=3π/2

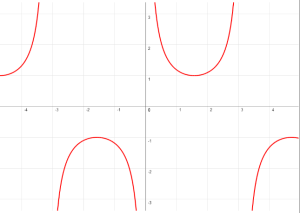
CARACTERÍSTICAS DE LA GRÁFICA DE  y = csc(x)

El ciclo fundamental de la función cosecante del ángulo comienza en 0 y termina en 2π.

Tiene tres asíntotas.

Dominio: el conjunto de números reales excepto los multiplos impares de π/2

Alcance: el conjunto de todos los números menores o iguales que -1 y todos los números mayores o iguales que1

Cruza el eje de “y” en (0,1)

El eje de referencia es: el eje “x”

El punto máximo es:   (π,-1)

El punto mínimo es: (0, 1)

Su período: 2π

Asíntotas: x=-π/2, x=π/2 y x=3π/2

RESUMEN DE LA LEY DE SENOS Y LEY DE LOS COSENOS

senos ley de lo Senos: La ley de los senos o teorema de los senos es una relación de proporcionalidad entre las longitudes de los lados de un triangulo y los senos de sus respectivos ángulos opuestos. Es útil para resolver problemas de triángulos oblicuángulos, es decir, aquellos que carecen de un ángulo recto (90°). Usualmente se presenta de la siguiente forma: “Si en un triangulo ABC, las medidas de los lados opuestos a los ángulos A, B y C son respectivamente a, b y c, entonces: “ 𝑎 𝑆𝑖𝑛𝐴 = 𝑏 𝑆𝑖𝑛𝐵 = 𝑐 𝑆𝑖𝑛𝐶 ” ” Tipos de triángulos en los que aplica la ley de los senos. La ley de los senos es aplicable en los triángulos oblicuángulos que son los que no tienen un ángulo de recto (90°), estos se dividen en:  Acutángulo: Es aquel que tiene los tres ángulos internos agudos, es decir, que miden menos de 90°.  Obtusángulo: Es aquel que tiene un ángulo obtuso, es decir que mide mas de 90°, mientras que los otros dos ángulos internos son agudos. 

cosenos Ley de los cosenos: Es una generalización del teorema de Pitágoras en los triángulos rectángulos que se utiliza, normalmente en trigonometría. El teorema relaciona un lado de un triangulo cualquiera con los otros lados y con el coseno del ángulo formando por estos dos lados. El teorema dice: Dado un triangulo ABC cualquiera, siendo 𝛼, 𝛽, 𝛾 los lados respectivamente opuestos a estos ángulos entonces: 𝑐2 = 𝑎2 + 𝑏2 − 2𝑎𝑏 cos 𝛾 Despejes de la formula: 𝑎2 = 𝑐2 + 𝑏2 − 2𝑏𝑐 cos 𝛼 𝑏2 = 𝑎2 + 𝑐2 − 2𝑎𝑐 cos 𝛽 Tipos de triángulos en los que aplica la ley de los cosenos. La ley de los cosenos es aplicable en los triángulos oblicuángulos que son los que no tienen un ángulo de recto (90°), estos se dividen en:  Acutángulo: Es aquel que tiene los tres ángulos internos agudos, es decir, que miden menos de 90°.  Obtusángulo: Es aquel que tiene un ángulo obtuso, es decir que mide mas de 90°, mientras que los otros dos ángulos internos son agudos.

ACTIVIDADES DEL LIBRO PAGINA 48

CALCULESE EL CATETO b SABIENDO QUE b=a x senB
 1.- a= 26.45, B= 37º,20'   
       b= a x sen B
       b= 26.45 * 0.60
       b= 15.91
 2.- a= 54.17, B= 58º 45'
      b= 54.17*0.84
      b= 45.93 

 3.- a= 32.27, B= 39º 50'
      b= 32.27*0.62
      b= 20.30 

  4.- a= 52.56, B= 37º 26'
       b= 52.56*0.60 
       b= 31.63

  5.- a= 125.34, B= 49º 37'
      b= 125.34*0.75
      b= 94.59 

   6.- a= 324.43, B= 17º 38'
        b= 324.43*0.29 
        b= 94.85

EJERCICIOS PAGINA 49. Calcular la hipotenusa, sabiendo que a= b/sen B
    7.- b= 42 B= 37º40' 
a= 42/0..62
a= 69                          

10.-b= 75. B=35º43'
 a= 75/0.57 
 a= 130.75

 8.- b= 56.48, B= 75º20'     
a= 56.48/0.96
a= 58.833

  11.-b= 37.40, B= 27º36'
a= 37.40/0.45
a= 82.38

 9.- b= 72.46, B= 35º40'   
a= 72.46/0.56
a= 127.12


  12.-b= 125.54, B= 36º57'   
  a= 125.5/0.58 
  a= 213.58         


                                                                      

c) calcule el angulo B, sabiendo que sen B= b/a
 13.- a=37.42, b=21,20 
    sen B= 21.20/37.42 
    sen B= 0.566

      16.- b= 32.44, a= 65.43     
         sen B= 32.44/65.43   
         sen B= 0.495                             

        14.- a= 56.81, b= 17.14
   sen B= 17.14/56.81 
   sen B= 0.30 


     17.- b= 12.21, a= 54.12
 sen B= 12.21/54.12   
 sen B= 0.225

    15.- a= 24.35 b= 8.93                     
sen B= 8.93/24.35
sen B= 0.366 


   18.- b=43.34, a= 45.48
  sen B= 43.34/45.48 
  sen B= 0.952

19.- Una escalera de 9m esta apoyada contra una pared. ¿que altura alcanza si forma con el suelo, supuesto horizontal, un angulo de 72º?   
 sen B= 72º   
  b=
 a= 9 m
 b= a*sen B
 b=  9*0.95
 b=8.55

20.- se inscribe un decagono regular en una circunferencia de 5cm de radio. Calcula la longitud del lado de dicho poligono. 
sen B= 36º
b= 5cm
a=
a= b/sen B 
a= 5/0.58   
a= 8.50