Proyecto de extraordinario de la materia de matemáticas para construir una iguana

 COLEGIO DE BACHILLERES DEL ESTADO DE OAXACA, COBAO PLANTEL 04 EL TULE 

NOMBRE: Josh Brandon Ruiz Cruz

MATEMÁTICAS 2

DOCENTE: Arquitecto Alejandro

SEGUNDO SEMESTRE

GRUPO: 205 

ELEMENTOS QUE UTILICE FUERON

– El teorema de Pitágoras

Dado un triángulo rectángulo con catetos «a», «b» e hipotenusa «c», se cumple que «c²=a²+b²».

– Área de triángulos

La fórmula para calcular el área de cualquier triángulo es A=(b×h)/2, donde «b» es la longitud de la base y «h» la longitud de la altura.

-Area de circulos y perimetros

El perímetro de un circulo es la circunferencia y su valor es igual diámetro multiplicado por pi. Como el diámetro es igual a dos radios también se puede decir que la longitud de la circunferencia = p x 2r

La razón (división) entre el perímetro y el diámetro de una circunferencia recibe el nombre de p (pi) y su valor aproximado es 3,14.

 

1.2- Área
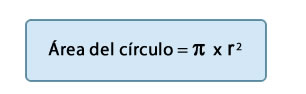
El área del círculo es igual al valor de su radio elevado al cuadrado multiplicado por pi = p x r².

– Ángulos de triángulos

La suma de los tres ángulos internos de un triángulo es 180º.

– Las funciones trigonométricas:

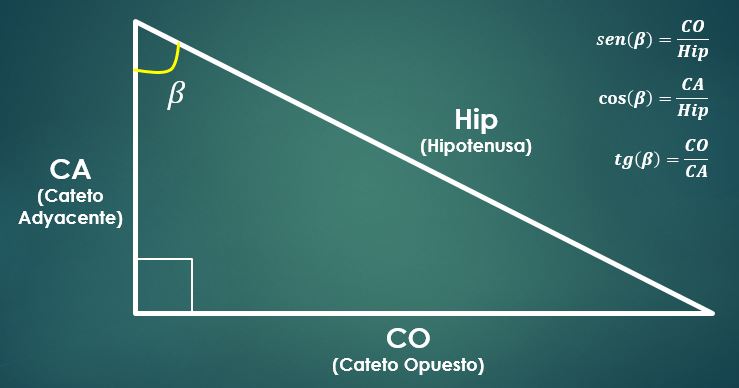
Considérese un triángulo rectángulo. Entonces, se definen las funciones trigonométricas seno, coseno y tangente del ángulo beta (β) como sigue:

sen(β) = CO/Hip,  cos(β)= CA/Hip  y tan(β)=CO/CA.

Ley de los cosenos

La ley de los cosenos establece: c ² = a ² + b ² – 2 ab cos C . Esto se parece al teorema de Pitágoras excepto que para el tercer término y si C es un ángulo recto el tercer término es igual 0 porque el coseno de 90° es 0 y se obtiene el teorema de Pitágoras.

El teorema del coseno, denominado también como ley de cosenos, ​ es una generalización del teorema de Pitágoras en los triángulos rectángulos en trigonometría. El teorema relaciona un lado de un triángulo cualquiera con los otros dos y con el coseno del ángulo formado por estos dos lados

pasar de grados a radianes paso a paso

Para pasar de grados a radianes lo hacemos mediante una regla de tres, teniendo en cuenta la equivalencia entre radianes y grados.

Por ejemplo, ¿cuántos radianes son 60º?

Planteamos la regla de tres: Si 180º son π radianes, 60º serán x radianes. Ponemos los grados debajo de los grados y los radianes debajo de los radianes:

Y ahora despejamos la x:

Ya sólo nos queda operar. Para dejarlo el resultado en múltiplos de π , simplificamos los números que tenemos en la operación y nos queda:

Por tanto, 60º equivalen a π /3 radianes:

Como te he comentado antes, no es obligatorio dejar los radianes en función de π , por lo que si te es más fácil, puedes sustituir π  por 3,14 y operar con la calculadora, cuyo resultado será:

conclusión

aprendí diversas funciones de las matemáticas, sus teoremas y formulas aplicándolas en la vida real e identificando que sirven no solo en la escuela sino en la vida diaria nos encontraremos con problemas igual de complicados y bastantes peores que podemos resolver fácilmente aplicando lo que acabo de aprender